Velkommen til dette forløb om sandsynlighedsregning og binomialfordelingen. I forløbet skal vi arbejde med tilfældigheder, bolde i forskellige farver, terningekast mm. I skal arbejde både praktisk og teoretisk, suppleret med små videoer, hvor teorien bliver forklaret.
Gennem simuleringer og eksperimentelt arbejde vil du blive klogere på tilfældighed og sandsynlighed, og du vil lære at løse forskellige typer af opgaver med sandsynlighedsregning. Du vil også lære om binomialfordelingen, som handler om forsøg med præcis to udfald: Succes eller fiasko.
Undervejs vil I også møde lidt af programmeringskoden bag simuleringerne og få lov til at eksperimentere med de indgående variable.
Vi starter med at møde Bastian, som elsker baseball… Velkommen til!
Projektet er en del af Dataekspeditioner.dk, som huses af Datalogisk Institut på Københavns Universitet og finansieres af Novo Nordisk Fonden.
Relevante faglige mål (med udgangspunkt i læreplanens § 2.1.):
- Operere med tal og repræsentationer af tal samt kritisk vurdere resultater af sådanne operationer
- håndtere formler, kunne opstille og redegøre for symbolholdige beskrivelser af variabelsammenhænge og kunne anvende symbolholdigt sprog til at løse problemer med matematisk indhold
- anvende statistiske og sandsynlighedsteoretiske modeller til beskrivelse af data fra andre fagområder, foretage simuleringer, gennemføre hypotesetest, bestemme konfidensintervaller, kunne stille spørgsmål ud fra modellen og have blik for, hvilke svar der kan forventes, samt være i stand til at formulere konklusioner i et klart sprog
- anvende matematiske værktøjsprogrammer til eksperimenter og begrebsudvikling samt symbolbehandling og problemløsning
- demonstrere viden om matematikanvendelse inden for udvalgte områder, herunder viden om anvendelse i behandling af en mere kompleks problemstilling
- demonstrere viden om matematikkens udvikling i samspil med den historiske, videnskabelige og kulturelle udvikling
- beherske mindstekrav omfattende grundlæggende matematiske færdigheder og kompetencer inden for kernestoffet
Afsnit 1 - Eksperimentel indledning
Bastian brænder for baseball! Han basker med battet og beder bare om Succes!
Bastians yndlingsfarve er orange, så for ham er Orange = Succes!
- Tryk på Start for at baske med battet, og se hvad der sker!
- Tryk på Pause for at observere hyppigheden af de to farver bolde.
- Kan I gætte, hvilken farve den næste bold har? Får Bastian Succes eller Fiasko i næste bask?
- Tryk Genstart for at begynde forfra.
- Er der et mønster?
Overvej undervejs følgende spørgsmål:
- Hvad er jeres bedste gæt på hyppigheden af Succes?
- Hvor mange bolde basker Bastian i hvert spil?
Når du er færdig med at spille, så tryk på Mark as complete-knappen for at komme videre til tjekspørgsmålene.
Besvar spørgsmålene:
Hvilken farve er Bastians yndlingsfarve?
- Orange
- Blå
Hvad er jeres bedste gæt på hyppigheden af Succes?
- 0%
- 25%
- 50%
- 75%
- 100%
Hvor mange bolde basker Bastian i hvert spil?
- 10
- 20
- 30
- 50
I denne øvelse skal I bruge papir og blyant samt en terning til at undersøge begreberne udfald, hyppighed og frekvens.
- Tegn ovenstående tabel på et stykke papir.
- Kast terningen 30 gange, og sæt for hvert kast en streg ud for det resulterende udfald.
- Tæl stregerne sammen, og skriv den samlede hyppighed for hvert udfald.
- Opret et tabel i Word/Excel eller lignende, og skriv hyppighederne ind i tabellen.
- Beregn frekvensen for hvert udfald, og skriv det i tabellen.
- Vis med et enkelt regneeksempel uden for tabellen, hvordan frekvensen beregnes.
- Tag et skærmklip af jeres besvarelse, og gem det.
I denne video præsenteres begreberne teoretisk sandsynlighed og sandsynlighedsfelt.
- Hvilke talværdier kan frekvensen have – er der en øvre og/eller nedre grænse?
- Får man nøjagtig det samme slutresultat hver gang? Hvorfor/hvorfor ikke?
- Hvilken Hyppighed svarer til Frekvensen 0?
- Hvilken Hyppighed svarer til Frekvensen 1?
- Efter at have kørt spillet mange gange skal I gætte på, hvilken frekvens, I mener, er den mest sandsynlige for udfaldet Orange/Succes?
- Hvis man kun kender frekvensen for Succes, S, kan man så beregne frekvensen for Fiasko, F? Hvordan?
Besvar spørgsmålene:
1: Hvordan beregnes frekvensen, og hvilken betydning har parameteren n?
- Skriv en forklaring med egne ord.
2: Hvilke af nedenstående værdier kan frekvensen antage? (Vælg alle de rigtige blandt flere mulige svar.)
- -1
- 0
- 1
- 0,5
- 1,5
- 2
3: Får man nøjagtigt det samme slutresultat hver gang?
- Ja
- Nej
4: Hvorfor/hvorfor ikke?
- Skriv en kort forklaring med egne ord.
5: Hvilken Hyppighed svarer til Frekvensen 0?
- 0
- 1
- 25
- 30
- 50
6: Hvilken Hyppighed svarer til Frekvensen 1?
- 0
- 1
- 25
- 30
- 50
7: Hvilken frekvens gætter I på, er den mest sandsynlige for udfaldet Orange/Succes?
- 0
- 1
- 0,25
- 0,8
- 0,50
8: Hvordan beregnes frekvensen for Fiasko, F, ud fra frekvensen for Succes, S?
- F = S
- F = 1 – S
- F = 1 + S
- F = S^2
I denne video præsenteres begreberne basisforsøg, succes og fiasko, binomialforsøg, binomialfordelt stokastisk variabel samt binomialmodel.
Som vi så i videoen, kan vi opstille en model for antallet af succeser (X) ud af n binomialforsøg.
X kaldes en stokastisk variabel og er styret af tilfældighed.
Vi siger, at ”X er en binomialfordelt stokastisk variabel med antalsparameter n og sandsynlighedsparameter p.”
Dette kaldes en binomialmodel og skrives således med matematisk notation: X \sim b(n,p)
Lav følgende opgaver to og to i et dokument på computeren.
Opgave 1
Amalie, Bertram og Caroline spiller rollespil og slår med en ottesidet terning.
a) Hvilke mulige udfald er der for hvert slag med terningen?
b) Hvad er den teoretiske sandsynlighed for hvert udfald?
c) Opstil et sandsynlighedsfelt (det vil sige tegn en tabel) over situationen.
d) Hvilken værdi har sandsynlighedsparameteren (p) her?
Opgave 2
Efter 10 min. rollespil har deltagerne tilsammen slået følgende slag med den ottesidede terning:
5 – 6 – 2 – 8 – 8 – 1 – 7 – 3 – 7 – 2 (og Bertram har vundet slaget mod dragen!).
a) Hvad er hyppigheden af udfaldet 8?
b) Hvad er hyppigheden af udfaldet 4?
c) Hvilken værdi har antalsparameteren (n) her?
d) Opstil en tabel over hyppighed og beregnet frekvens for situationen.
Opgave 3
a) Er der overensstemmelse mellem de teoretiske sandsynligheder fra Opgave 1b og de observerede frekvenser i Opgave 2c?
b) Hvorfor/hvorfor ikke?
Afsnit 2 - Mød koden bag programmet!
I det foregående modul har vi eksperimenteret med boldkast og undersøgt begreberne
hyppighed og frekvens.
Eksperimenterne kaldes også en simulering af data.
Vi lærte også om den teoretiske sandsynlighed og om begrebet en binomialfordelt stokastisk variabel, samt mødte begrebet en binomialmodel: X \sim (n,p).
Vi lærte, at antallet af succeser i en række kast med en bold er binomialfordelt med antalsparameter n og sandsynlighedsparameter p.
I dette modul skal vi ved hjælp af flere simuleringer undersøge parametrene n og p lidt nærmere, og derved forhåbentlig nærme os en forståelse af binomialfordelingen.
I kan nu se lidt af koden bag boldspillet til højre i vinduet.
Vi skal prøve at lege lidt med sandsynlighedsparameteren p:
Spil spillet flere gange med forskellige værdier af p.
NB Tryk Genstart for at aktivere et ændret input af p.
Kør spillet helt til ende hver gang. Pas på, at I ikke går for hurtigt videre.
Hvis I ændrer p-værdien, skal I trykke Genstart for at aktivere ændringen.
Hvis programmet driller, så genstart siden ved at trykke på F5 (På Mac: Cmnd + R).
Overvej følgende spørgsmål undervejs:
- Hvilken betydning har p for udfaldet af spillet?
- Er der forskel på frekvensen i starten og slutningen af spillet? Hvorfor mon?
- Hvilke værdier kan p antage? Er det nogle grænser for værdien af p?
Besvar spørgsmålene på næste side, når I er klar.
Besvar spørgsmålene:
1: Hvilke værdier kan p antage? Der er flere mulige svar – vælg alle de rigtige svar.
- 0
- 1
- 0,75
- 2
- -1
- 25
2: Er der forskel på frekvensen i starten og slutningen af spillet?
- Skriv en kort tekst, hvor I beskriver, hvad I ser i spillet.
3: Hvilke værdier kan p antage – er der nogen grænser for værdien af p?
- Skriv en kort tekst.
4: Spørgsmål til koden:
- Hvilken værdi har n (eller kan I selv vælge)?
- Hvilken værdi har p (eller kan I selv vælge)?
5: Prøv at forklare, hvad der sker i nogle af kodelinjerne.
I denne video lærer du om symmetrisk og asymmetrisk sandsynlighedsfelt.
I kan nu også ændre værdien af parameteren n.
NB Tryk Genstart for at aktivere et ændret input af n eller p.
Prøv at undersøge situationer med forskellige værdier af n og p. Kør programmet til ende (med mindre I har valgt en meget stor n-værdi!).
Hvis programmet driller, så genstart siden ved at trykke på F5 (På Mac: Cmnd + R).
Overvej følgende spørgsmål, som skal besvares i den efterfølgende quiz:
- Hvilken betydning har n for resultatet?
- Hvilke værdier kan n antage? Eller er der nogle værdier, n ikke kan antage?
- Hvornår kommer frekvensen for succes tættest på p – når n er lille, eller når n er stor? Hvorfor?
- Kig godt på koden, og prøv at forklare, hvad I tror, de enkelte linjer i koden betyder – evt. bare nogle af linjerne.
Besvar spørgsmålene
1: Hvilken betydning har n?
- Skriv en forklaring med egne ord.
2: Hvilke værdier kan n antage? Er der nogen værdier, n ikke kan antage?
- Skriv en forklaring med egne ord.
3: Hvornår kommer frekvensen for Succes tættest på p – når n er lille eller når n er stor? Hvorfor?
- Skriv en forklaring med egne ord.
4: Kig godt på koden. Prøv forklare, hvad I tror, de enkelte linjer i koden betyder – evt. bare nogle af linjerne.
Middelværdi
Hvis et binomialforsøg gentages mange gange, kalder vi det en hændelse, og vi kan så beregne det gennemsnitlige antal succeser som: n \times p.
Dette kaldes også middelværdien og betegnes med det græske bogstav \mu (lille my).
Altså: \mu = n \times p.
Middelværdien angiver det mest sandsynlige antal succeser, man vil få, hvis man gennemfører et binomialforsøg mange gange efter hinanden.
Eksempel: Bastian kaster 16 baseball-bolde (n = 16), og sandsynligheden for at få en orange bold i hvert kast er 0.5 (p = 0.5). Middelværdien er: \mu = 16 \times 0.5 = 8.
Spredning
Spredningen er et udtryk for variationen i resultaterne og betegnes med det græske bogstav \sigma (lille sigma).
Spredningen beregnes med formlen \sigma = \sqrt{n \times p \times (1 – p)}
Eksempel: n = 16 og p = 0.5. Spredningen er: \sigma = \sqrt{16 \times 0.5 \times (1 – 0.5)} = 4.
Opgave 1
En stokastisk variabel, X, er binomialfordelt med antalsparameter 12 og sandsynlighedsparameter 0,6.
- Opstil en binomialmodel for situationen – benyt korrekt notation.
- Beregn middelværdien, \mu, og spredningen, \sigma (lommeregner er tilladt).
(Facit: \mu = 7,2, \sigma = 2,88)
Opgave 2
Jens køber 30 tulipanløg på en planteskole. Planteskolen lover, at ud af de 50 løg vil gennemsnitligt 45 løg spire.
- Hvilket udfald svarer her til succes, og hvilket svarer til fiasko?
- Hvad er sandsynligheden for succes?
- Indfør en stokastisk variabel, og opstil en binomialmodel.
- Beregn middelværdien ud fra formlen ovenfor – passer det med oplysningerne i opgaven?
- Beregn spredningen.
Her er nogle eksempler på tidligere stillede eksamensopgaver (STX Mat B) uden hjælpemidler.
Formelsamling er eneste tilladte hjælpemiddel.
Opgave 1
Opgave 2
Opgave 3
Opgave 4
- Hvad er forskellen på Næste og Prøv igen?
- Hvad kan man observere i tabellen, når man trykker på Prøv igen flere gange efter hinanden?
- Hvad viser tabellen til højre?
- Hvilken værdi tror I, at p har?
- Vend tilbage til n = 1, og tryk gentagne gange på Prøv igen. Hvilke frekvenser får I?
- Prøv med n = 2, og tryk gentagne gange på Prøv igen. Hvilke frekvenser får I nu?
- For n = 3?
- For n = 10?
- For hvilken n-værdi kan I give det bedste gæt på den valgte p-værdi?
Besvar spørgemålene
Skriv en forklaring med egne ord med svar på følgende:
- Hvad er forskellen på Næste og Prøv igen?
- Hvad kan man observere i tabellen, når man trykker på Prøv igen flere gange efter hinanden?
- Hvad viser tabellen til højre?
- Vend tilbage til n = 1 og tryk gentagne gange på Prøv igen. Hvilke frekvenser får I?
- Prøv med n = 2, og tryk gentagne gange på Prøv igen. Hvilke frekvenser får I nu?
- For n = 3?
- For n = 10?
- Hvilke værdier kan hyppigheden antage? Hvad er summen af de to tal? Hvorfor er det tal interessant?
- Relateret til spørgsmål 1: Hvilken værdi har n?
- Hvilke værdier kan frekvensen antage?
- Hvilken værdi gætter I på at p har? Hvorfor?
- Hvad viser tabellen til højre?
- Hvad sker der i tabellen, hvis I trykker rigtigt mange gange på Start? Og relateret hertil:
- Hvad er den mest almindelige/hyppige værdi af hyppighed?
Besvar spørgemålene
Skriv en forklaring med egne ord med svar på følgende:
- Hvilke værdier kan Hyppigheden antage? Hvad er summen af de to tal (Hyppigheden for Gul/Succes og Hyppigheden for Blå/Fiasko)? Hvorfor er det tal interessant?
- Relateret til spørgsmål 1: Hvilken værdi har n?
- Hvilke værdier kan Frekvensen antage?
- Hvilken værdi gætter I på at p har? Hvorfor?
- Hvad viser tabellen til højre?
- Hvad sker der i tabellen, hvis I trykker rigtigt mange gange på start?
Afsnit 3 - Sandsynlighedsfunktion
På den sidste tabel i Afsnit 2 gættede I forhåbentlig på, at n var 10 og p var 0,5.
Vi fortsætter med at gentage dette binomialforsøg, hvor n = 10 og p=0,5, dvs X \sim b(10,0.5).
Ét forsøg er altså 10 kast og i hvert af de 10 kast er der 50% chance for at få en orange bold (Succes).
Vi gentager nu dette forsøg flere gange. Antallet af gentagelser kalder vi for m.
- Tryk på m=1, og diskuter, hvad der sker – dels på søjlediagrammet, dels i tabellen til højre.
- Hvad viser akserne i diagrammet?
- Hvad viser kolonnerne i tabellen?
- Tryk på m=1 flere gange, og diskuter, hvad der sker. Hvor mange bolde kastes, hvor mange orange bolde er der i hvert forsøg, osv.
- Efter 5 tryk låser knappen m=10 op. Fortsæt med at trykke på knapperne, og diskuter, hvad der sker. Hvorfor får I ikke det samme resultat hver gang?
- For m=1000: Prøv at formulere en sætning eller to, der forklarer både søjlediagrammet og tabellen.
- Hvad sker der med søjlediagrammet, når m vokser – er der en form for mønster?
Binomialkoefficient
Fra kombinatorikken kender vi udtrykket K(n,r), som betegner antal måder, hvorpå man kan udvælge relementer blandt i alt n elementer, når rækkefølgen ikke har betydning.
K(n,r) = \frac{n!}{r!(n-r)!}
Udtrykket K(n,r) kaldes også for en binomialkoefficient og skrives:
K(n,r) = {n \choose r}= \frac{n!}{r!(n-r)!}
CAS-kommandoer, K(n,r)
TI-Nspire: ncr(n,r)
Maple: 1. with(Gym); 2. binomial(n,r)
Eksempel 1
Spørgsmål: På hvor mange måder kan der vælges 2 elever til elevrådet i en klasse med 25 elever?
Svar: K(25,2) = \frac{25!}{2!(25-2)!} = … beregnes således:
CAS: TI-Nspire: … ncr(25,2) = 300 måder. Eller: Maple: … binomial(25,2) = 300 måder.
Eksempel 2
På hvor mange måder kan Bastian få 7 orange bolde ud af i alt 10 kast?
Svar: K(10,7) = \frac{10!}{7!(10-7)!} = 120 måder.
Prøv selv: Opgave 1
Partiet “Vi elsker matematik” har i alt 46 opstillede kandidater til det kommende valg. På hvor mange måder kan der vælges 3 matematikere ud af de opstillede kandidater?
Prøv selv: Opgave 2
Vi kan ganske vist ikke se forskel på Bastians bolde, men vi kan observere, hvilken farve bold nr. 1, 2 osv. har. Vi kan derfor stille følgende spørgsmål: På hvor mange måder kan Bastian få 4 orange bolde ud af i alt 10 kast?
Facit:
Opgave 1: 15180
Opgave 2: 210
Sandsynlighedsfunktionen for en binomialfordelt stokastisk variabel X
Binomialkoefficienten bruges til at beregne sandsynligheder i binomialfordelingen.
Hvis en stokastisk variabel, X, er binomialfordelt: X \sim b(n,p), beregnes sandsynligheden for at få præcis r succeser ud af n basisforsøg således:
P(X=r) = K(n,r) \times p^r \times (1-p)^{n-r}
Dette kaldes også for en punktsandsynlighed, og er altid et tal mellem 0 og 1 (svarende til 0-100%).
CAS-kommandoer, Punktsandsynligheder, P(X = r)
TI-Nspire: binompdf(n,p,r)
Maple: 1. with(Gym); 2. binpdf(n,p,r)
NB “binompdf” eller “binpdf” står for “Binomial Probability Distributional Function”.
Eksempel 1 – Sandsynlighed
Sandsynligheden for at få præcis 4 orange bolde ud af de 10 kast (n=10, p=0.5, r=4), er:
P(X=4) = K(10, 0.5) \times 0.5^4 \times (1-0.5)^{10-4} = 0,205=20,5 %
Vi vil altså forvente at få præcis 4 succeser i 0,205 = 20,5 % af tilfældene.
Eksempel 2 – Forventet antal succeser, m = 10
Ud fra punktsandsynlighederne kan vi beregne det forventede antal succeser ud af en række forsøg.
Lad os gentage binomialforsøget 10 gange (m=10). I hver af de 10 runder er der 20,5% chance for at få præcis 4 orange bolde. Beregning: 10 \times P(X=4) = 10 \times 0,205 = 2,05.
Altså vil vi forvente at få præcis 4 succeser ca. 2,05 gange ud af de 10 runder.
Eksempel 3 – Forventet antal succes’er, m = 100
Nu gentager vi forsøget med de 10 kast 100 gange (m=100). Hvor mange gange ud af de 100 vil vi forvente at få præcis 2 succeser ud af 10 kast?
Svar: 100 \times P(X=2) = 100 \times 0.0439 = 4,39
Altså vil vi forvente at få præcis 2 succeser ca. 4,39 gange ud af de 100 runder.
Disse beregninger skal bruges senere, når vi ser på søjlediagrammer med forventede værdier.
Her er nogle opgaver med formlen:
P(X=r) = K(n,r) \times p^r \times (1-p)^{n-r}
Facit til nogle af opgaverne ses nederst på siden.
Opgaver uden hjælpemidler – brug papir og blyant!
Opgave 1
Opgave 2
Opgaver med hjælpemidler
Husk CAS-kommandoerne for P(X = r):
TI-Nspire: binompdf(n,p,r)
Maple: 1. with(Gym); 2. binpdf(n,p,r)
Opgave 1 (Sandsynligheder)
Vi ser på boldspillet, hvor n=10 og p=0.5. Beregn med et CAS-værktøj følgende sandsynligheder:
- P(X=0)
- P(X=5)
- P(X=10)
Opgave 2 (Sandsynligheder)
I forlængelse af opgave 1 udfyldes ved hjælp af CAS en tabel af denne type. Afrund til 3 decimalers nøjagtighed.
Tip: Tabellen kan oprettes i et regneark i Nspire ved hjælp af formlen = binompdf(10,0.5,r) .
| r | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(X=r) |
Er der noget, I bemærker om de beregnede tal – et mønster?
Hvilken værdi har den højeste sandsynlighed?
Opgave 3 (Forventede antal succeser)
Vi bliver i boldspil-situationen:
Lad m=10, n=10, p=0.5 og r=3.
Beregn det forventede antal succeser for dette tilfælde, og forklar med ord, hvad der menes med dette.
Tip: Se Eksempel 2 på forrige side.
Opgave 4 (Forventede antal succeser)
Vi antager nu, at forsøget med de 10 kast gentages m=100 gange.
- Hvor mange gange vil vi forvente at få præcis 5 succeser? Vis beregning.
- Hvor mange gange vil vi forvente at få præcis 10 succeser? Vis beregning.
Opgave 5 (Forventede antal succes’er)
I forlængelse af opgave 4 udfyldes en tabel af denne type ( m=100, n=10, p=0,5). Afrund til 2 decimalers nøjagtighed.
| r | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Forv. |
Denne tabel skal vi bruge på næste side!
Ekstra-opgave (i forlængelse af se opgave 3)
Lad m=30, n=8, p=0,6 og r=4.
Beregn det forventede antal succeser for dette tilfælde, og forklar med ord, hvad der menes med dette.
Vi skal nu bruge vores beregninger af forventede værdier fra de to foregående sider om sandsynlighedsfunktion.
Gå evt. tilbage og repeter eksempler og opgaver, hvis I bliver i tvivl undervejs.
Klik på m=100 og diskuter, hvad I ser ud fra de næste spørgsmål:
- Hvad er der ud ad x-aksen?
- Hvad er der op ad y-aksen?
- Hvad repræsenterer de blå søjler? (Se Opgave 5 på forrige side.)
- Hvad repræsenterer de grønne søjler? Hvorfor er der forskel på de blå og de grønne søjler?
- Tryk gentagne gange på m=100 – hvad sker der?
- Hvad sker der med akserne, når værdien af m vokser?
- Hvad sker der med værdien af de blå og grønne søjler, når værdien af m vokser?
- Hvad sker der med forskellen på en blå og en grøn søjle (for hver værdi på x-aksen), når værdien af m vokser? Hvorfor?
I forrige aktivitet kunne I observere, at forskellen på de blå og de grønne søjler blev mindre, når mvoksede. Eller sagt lidt mere formelt:
Store Tals Lov
Når antallet af forsøg (m) vokser, vil antallet af observerede succeser nærme sig antallet af forventede succeser.
Læs lige sætningen et par gange! Gå derefter tilbage til søjlediagrammet på forrige side, og undersøg, om det ser ud til at passe.
Diskuter følgende spørgsmål med din sidemakker:
- Hvad er de vigtigste pointer i Afsnit 3? Hvilke nye begreber møder I?
- Kan du gøre rede for betydningen af de begreber, I har skrevet i spørgsmål 1?
- Prøv at sætte ord på, hvad I har lært af de to aktiviteter med søjlediagrammer? En konklusion?
- Hvad siger Store Tals Lov?
Binomialkoefficient, K(n,r)
TI-Nspire: ncr(n,r)
Maple: 1. with(Gym); 2. binomial(n,r)
Punktsandsynligheder, P(X = r)
TI-Nspire: binompdf(n,p,r)
Maple: 1. with(Gym); 2. binpdf(n,r)
Sandsynlighedstabel og søjlediagram
TI-Nspire: (video 0-3.10 min.):
Afsnit 4 - Kumulerede sandsynligheder
Sandsynlighedsfunktion eller punktsandsynlighed
Som vi har lært, er P(X=4) sandsynligheden for at få præcis 4 succeser ud af n = 10 forsøg. Dette kaldes for en punktsandsynlighed.
Kumuleret sandsynlighed
Ud fra punktsandsynlighederne kan vi beregne de såkaldte kumulerede sandsynligheder.
Vi antager fortsat, at n=10 og p=0.5.
1. Sandsynligheden for at få højst 2 succeser beregnes som summen af punktsandsynlighederne for 0, 1 og 2:
P(X \le 2) = P(X = 0) + P(X = 1) + P(X = 2)=0.00098+0.00977+0.04395=0.05469
2. Sandsynligheden for at få mindst 8 succes’er:
P(X \ge 8) = P(X = 8) + P(X = 9) + P(X = 10) = 0.05469 eller: P(X \ge 8) = 1 – P(X \le 7) = 0.05469
3. Sandsynligheden for at få mindst 2 og højst 4 succes’er:
P(2 \le X \le 4) = P(X = 2) + P(X = 3) + P(X = 4)=0.366
CAS-kommandoer, kumulerede sandsynligheder
TI-Nspire:
P(X \le r) = binomcdf(n,p,r)
P(X \ge r) = binomcdf(n,p,r,n)
P(r1 \le X \le r2) = binomcdf(n,p,r1,r2)
Maple: 1. with(Gym); 2. Som ovenfor, blot med bincdf i stedet for binomcdf.
NB “binomcdf” eller “bincdf” står for “Binomial Cumulative Probability Distributional Function”.
Her er nogle opgaver med kumulerede sandsynligheder. Facit ses nederst på siden.
Opgaver med CAS
Se kommandoerne til TI-Nspire og Maple nedenfor.
Afrund til 3 decimalers nøjagtighed.
Opgave 1
Antag, at n=10 og p = 0.5. Beregn den kumulerede sandsynlighed P(X \le 7).
Opgave 2
Beregn sandsynligheden for, at Bastian får mindst 5 orange bolde ud af 10 kast.
Opgave 3
Beregn sandsynligheden for, at Bastian får mellem 3 og 8 orange bolde ud af 10 kast.
Opgave 4
En stokastisk variabel X er binomialfordelt X \sim b(40,0.1).
Bestem P(X \le 4).
CAS-kommandoer, kumulerede sandsynligheder
TI-Nspire:
P(X \le r) = binomcdf(n,p,r)
P(X \ge r) = binomcdf(n,p,r,n)
P(r1 \le X \le r2) = binomcdf(n,p,r1,r2)
Maple: 1. with(Gym); 2. Som ovenfor, blot med bincdf i stedet for binomcdf.
Opgaver uden CAS
Lav først opgave 5, dernæst opgave 6 (de hænger sammen).
Opgave 5
Hvad er P(0 \le X \le n), uanset værdien af n?
Opgave 6
En stokastisk variabel X er binomialfordelt med antalsparameter 12 og en ukendt sandsynlighedsparameter p.
To af sandsynlighederne for X er bestemt ved P(X \le 7) = 0.56 og P(X \ge 9) = 0.23.
Bestem sandsynligheden P(X = 8).
Facit
Opgave 1: 0.945
Opgave 2: 0.623
Opgave 3: 0.935
Opgave 4: 0.629
Opgave 5: 1
Opgave 6: 0.21
- Hvad viser diagrammet og hvad er der ud af akserne?
- Hvad sker der, når du ændrer værdien af p? Hvorfor? Tag udgangspunkt i eksemplet med Bastian, der spiller baseball og prøv at forklare med ord, hvad er sker.
- Programmet har indbygget nogle begrænsninger (max/min) for de indtastede værdier af p – hvilke?
- Hvad sker der, når du ændrer værdien af j (=n)? Hvorfor?
- Hvilke begrænsninger er der for de indtastede værdier af j (max/min)?
- Hvad sker der, når du ændrer værdien af i (=m)? Hvorfor?
- Hvilke begrænsninger er der for de indtastede værdier af i (max/min)?
- Diskuter, hvad de enkelte linjer i koden mon betyder.
- Denne gang indeholder koden to løkker, der er indlejret i hinanden – dette er markeret med rød og orange farve. Prøv at diskutere med din sidemakker, hvad de to løkker gør. Hvad er det smarte ved opbygningen af kode på denne måde?
Afsnit 5 - Normalfordelingsapproksimation
Simulering
Vi ser her søjlediagrammet med de forventede (blå) og simulerede (grønne) værdier for 1000 gentagelser af Bastians kast med 10 bolde.
- Tryk på Start, og diskuter med din sidemakker, hvad der sker.
- Hvilke værdier har parametrene p, n og m?
- Hvad sker der, hver gang man trykker på Start?
I et binomialfordelt datasæt (de blå søjler) kan data kun antage hel-tallige værdier, nemlig et bestemt antal succeser pr. hændelse. Den slags data kaldes diskrete.
Den røde, klokkeformede kurve på figuren kaldes en Normalfordeling.
I et normalfordelt datasæt (den røde kurve) kan der forekomme alle mulige forskellige tal, også decimaltal. Den slags data kaldes kontinuerte.
Normalfordelingsapproksimation
En normalfordeling er symmetrisk omkring middelværdien. Det er binomialfordelingen ikke altid. Hvis p er meget lille eller meget stor, bliver binomialfordelingen skæv og er derfor vanskelig af approksimere med en normalfordeling. Man bruger tommelfingerreglen, at når både n \times p \gt 5 og n \times (1 – p) \gt 5, kan man bruge approksimationen, det vil sige at de binomialfordelte data (de blå søjler) tilnærmelsesvist ligner normalfordelte data (den røde kurve).
Opgave 1
En stokastisk variabel X er binomialfordelt X \sim b(40,0.1).
Kan normalfordelingsapproksimationen benyttes i dette tilfælde?
Middelværdi og spredning
Vi husker, at formlerne for middelværdi og spredning er:
Middelværdi: \mu = n \times p.
Spredning: \sigma = \sqrt{n \times p \times (1 – p)}
I vores eksempel – X \sim b(10,0.5) – er middelværdien: \mu = n \times p = 10 \times 0.5 = 5
– og spredningen er: \sigma = \sqrt{n \times p \times (1 – p)} = \sqrt{10 \times 0.5 \times (1 – 0.5)} \approx 1.58.
Opgave 2
Beregn \mu-2\cdot\sigma og \mu+2\cdot\sigma, og sammenlign med figuren ovenfor. Ligger markeringerne nogenlunde korrekt placeret under x-aksen?
Facit
Opgave 1: Nej, fordi n \times p = 4.
Opgave 2: \mu-2\cdot\sigma = 1.84, \mu+2\cdot\sigma=8.16. Ja.
Normale og exceptionelle udfald
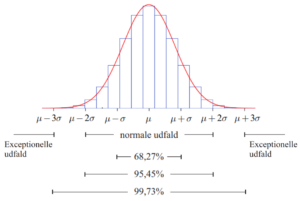
Teori
I normalfordelingen gælder altid, at:
68,27% af observationerne ligger i intervallet \mu \pm \sigma.
95,45% af observationerne ligger i intervallet [\mu – 2\sigma;\mu + 2\sigma].
99,73% af observationerne ligger i intervallet [\mu – 3\sigma;\mu + 3\sigma].
Normale udfald er de 95,45 % af alle udfald, der ligger i intervallet [\mu – 2\sigma;\mu + 2\sigma].
Exceptionelle udfald er udfald, der er mindre end \mu – 3\sigma eller større end \mu + 3\sigma.
Exceptionelle udfald udgør altså 100 – 99.73 = 0.27% af observationerne.
I binomialfordelingen kan vi benytte de samme procentsatser og betegnelser, under forudsætning af, at n \times p \gt 5 og n \times (1 – p) \gt 5. Da der som sagt kun er tale om hel-tallige værdier i binomialfordelingen, skal vi dog afrunde til hele tal. Se eksemplerne nedenfor.
Eksempler
I vores eksempel – X \sim b(10,0.5) – er: \mu = 5 og \sigma \approx 1.58.
Lad os betragte intervallet: \mu \pm \sigma = [5 – 1.58 ; 5 + 1.58] = [3.41;6.58].
Vi afrunder til hele tal på følgende måde: Det mindste tal rundes op, og det største tal rundes ned. Her skal 3,41 altså rundes op til 4 og 6,58 skal rundes ned til 6.
Normalfordelingsapproksimationen fortæller os således, at vi kan forvente at ca. 68% ligger i intervallet [4,6]. Hvis vi regner efter med binomialfordelingen, får vi at 65,6% af observationerne skal ligge i intervallet [4,6]. Da 65.6% er tæt på 68.27% kan vi se, at normalfordelingsapproksimationen giver os et godt bud på, hvor mange udfald vi forventer at få i intervallet.
Normale udfald, eksempel:
I vores eksempel ligger de normale udfald i intervallet: [\mu – 2\sigma;\mu + 2\sigma] = [1.84;8.16].
Igen skal det mindste tal rundes op og det største tal rundes ned.
Konklusion: “Normale udfald” er her alle udfald i intervallet [2;8].
Exceptionelle udfald, eksempel:
I eksemplet er \mu -3\sigma = 0.26 og \mu + 3\sigma = 9.74.
For at finde de exceptionelle udfald, skal vi se på heltallige udfald, der er mindre end 0.26 eller større end 9.74. Her skal 0,26 altså rundes ned til 0 og 9,74 skal rundes op til 10.
Konklusion: “Exceptionelle udfald” er altså i dette eksempel kun udfaldene 0 og 10.
Opgave 1
En stokastisk variabel X er binomialfordelt X \sim b(50,0.7).
- Kan normalfordelingsapproksimationen benyttes i dette tilfælde?
- Angiv middelværdi og spredning.
- Angiv intervallet for normale udfald samt de to intervaller for exceptionelle udfald. Husk at svarene skal være hele tal, ikke decimaltal.
Facit
Opgave 1.1: Ja, fordi n \times p = 35 og n \times (1 – p) = 15
Opgave 1.2: \mu = 35, \sigma = 3.24.
Opgave 1.3: Normale udfald = [29;41], Exceptionelle udfald = [0;25] og [45;50].
Her er et par eksempler på mundtlige eksamensspørgsmål, som er beregnet til den individuelle delprøve på Matematik B, stx.
Spørgsmål 1
Forklar, hvad der forstås ved en binomialfordelt stokastisk variabel. Kom herunder ind på begreberne antalsparameter, sandsynlighedsparameter, middelværdi og spredning. Inddrag et eller flere selvvalgte taleksempler.
Tegn et pindediagram for en binomialfordelt stokastisk variabel, og vis, hvordan man kan aflæse binomialsandsynligheder at typen P(X = r).
Forklar desuden begreberne normale udfald og exceptionelle udfald med udgangspunkt i pindediagrammet.
Spørgsmål 2
Forklar, hvad der forstås ved en binomialfordelt stokastisk variabel, samt hvordan man beregner middelværdi og spredning. Inddrag et eller flere selvvalgte taleksempler.
Forklar, hvad en binomialkoefficient, K(n,r), er, hvordan den beregnes, samt hvordan man i den sammenhæng anvender Pascals trekant.
Forklar, hvad der forstås ved binomialsandsynligheder af typen P(X=r), P(X \le r) og P(X \ge r), samt hvordan man beregner disse. Inddrag et eller flere selvvalgte taleksempler.
Afslutning
Konklusion
Du har i dette forløb lært om sandsynlighedsregning og binomialfordelingen gennem simuleringer og opgaver. Du har også snuset lidt til programmering og computational thinking.
Du har lært om følgende begreber fra læreplanen for Matematik B (STX):
- Udfald, hyppighed og frekvens
- Teoretisk/forventet sandsynlighed i modsætning til observeret sandsynlighed
- Symmetrisk og asymmetrisk sandsynlighedsfelt
- Stokastisk variabel
- Binomialmodel: X \sim (n,p)
- Antalsparameter (n) og sandsynlighedsparameter (p)
- Middelværdi og spredning
- Sandsynlighedsfunktion: P(X = r) = K(n,r) \times p^r \times (1 – p)^{n-r},
- Store Tals Lov
- Normalfordelingsapproksimation
- Normale og exceptionelle udfald.
Derudover skal du på matematik B også kende til binomialtest og konfidensintervaller, som dog ikke indgår i dette forløb.
Tak fordi du fulgte med. 
Mischa Sloth Carlsen 
Cecilie Bepler 
Birgitte Wandall